On va parler un peu de mathématique, rapidement aborder la théorie des graphes et les bases numériques. Pour optimiser les calculs. On va le faire visuellement.
Tout d'abord la théorie des graphes. La théorie des graphes est une branche des mathématiques et de l'informatique qui étudie les graphes, des structures composées de nœuds (aussi appelés sommets) reliés par des arêtes (ou liens). Ces structures sont utilisées pour modéliser des relations entre des entités ou des objets.
On peut considérer qu'un ensemble de nombre peut être modéliser entre eux. Et donc il y a des relations.
Par exemple le carré magique d'ordre 3. On modélise une grille avec des nombres de 1 à 9. les nombres on un espace. Ils sont dans une case et leur relation peut donner des propriétés remarquables. C'est à dire qu'il y a des noeuds.
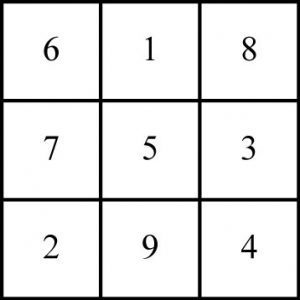
- Les nombres peuvent être placer dans une grille: c'est l'espace
- Les nombres sont des suites numériques ordonnées tel un compteur: c'est le temps
Vous avez le principe de l'espace-temps. Pour que le temps soit défini il faut une horloge, un principe circulaire dans un espace. C'est à dire que les nombres formes la plus petites figures circulaires possibles. Si on met en lien avec des sommets cela donne le triangle qui défini des noeuds. Et il y a des relations de contraintes et propriété géométrique dans notre triangle.
Quel est le lien en théorie des graphes avec le temps et donc la relativité? En théorie des graphes, le temps peut-être modelisé comme un concept topologique, surtout dans le cadre des graphes orientés ou les arêtes peuvent représenter des transitions d'un état à un autre. Cela se produit par des évenements discrets temporelles. La relativité du temps peut être illustrée dans les graphes à travers des réseaux temporels, où le temps de traversée d’une arête (d'un événement à l'autre) peut varier selon les observateurs ou selon les contraintes physiques comme la vitesse ou la gravité. C'est un problème de localisation sur grille.... L'observateur est local.
C'est ce que l'on appel des problèmes de synchronisation. Par exemple prenons le cas des serveurs, vous connaissez le protocole NTP, on synchronise le temps entre des machines. Car toutes machines indépendantes sur son propre réseau subit une perte de synchronisation locale, un décalage reflétant que le temps est relatif à chaque machine. On parle alors d'algorithme de Lamport pour générer cette relativité. Il utilise le "Timestamps" pour ordonner des évenement sur le réseau.
Quel est le rapport donc avec les bases numériques? On parle de dilatation. Et de complexité algorithmique. C'est un problème de stabilité pour la synchronisation. Un peu comme des problèmes insolubles tel que la quadrature du cercle.
Certaine base en théorie des graphes sont plus facile pour la modelisation que d'autres. Et donc facilite le système d'encodage et les fonctions de hashages pour optimiser les calculs.
C'est la petite guerre d'église par exemple pour le maillage dans nos théorie des graphes pour la modélisation. C'est à dire des formes d'analyse matricielle des structures. Les structures sont élastiques et subissent des déformations tels que les calcules par la méthode des éléments finis. On utilise un système de maillage basé sur des triangles. on défini un pavage qui sont des élements finis. Et donc le maillage tetraedrique permet de mailler de façon fidèle les géométries complexes.
Hors il y a une petite guerre de religion, l'apparition du pixel. Qui est un changement de base. On passe de la base 3² (trinitaire) à la base 4² (quaternaire). Du triangle au carré... Et donc des problèmes de diviseurs... Mais aussi de puissance...
Base 9:
- Facteurs premiers: 3²
- Diviseurs: 1, 3, 9
- Système de numération: base 9
Base 16:
- Facteurs premiers: 2⁴
- Diviseurs: 1, 2, 4, 8, 16
- Système de numération: hexadécimal
En théorie de modélisation, c'est un problème de bloc. Il est plus simple de modéliser à partir d'un cube que d'un tetraedre question de volumétrie. C'est un problème de pile... Et donc de résolution de problème de construction. Dans la théorie des graphes, nos noeuds peuvent prendre du volume et donc changer de dimension, et là c'est un problème de pile, d'ou que l'on intègre des blocs. On ne peut pas avec des tetraèdres.
Donc logiquement on devrait calculer en base quaternaire, la base 16 comme système carré en natif pour optimiser nos graphes. A cause de problème de pile.
En gros la modélisation par élément fini devient caduque en apportant une innovation radicale par les théories des graphes et la volumétrie par des piles.
C'est des problèmes de topologie avancée des formes et leur modélisation. Qui sont des problèmes de constructions...
Peut-être que vous avez fait le lien, avec le problème insoluble de la gravité. La prise de masse d'un noeud en théorie des graphes n'est qu'un problème de pile.
Cela pourrait donner des idées en recherche sur la gravité quantique ma théorie.